자료구조 분류
1. 단순구조
- 정수
- 실수
- 문자
- 문자열
2. 선형구조 // 자료들 사이의 관계가 1:1 관계
- 리스트
- 스택
- 큐
3. 비선형구조 // 자료들 사이의 관계가 1다 or 다:다 관계
- 트리
- 그래프
4. 파일구조 // 서로 관련 있는 필드로 구성된 레코드의 집한인 파일에 대한 구조
- 순차파일
- 색인파일
- 직접파일
추상 자료형 (Abstract Data Type, ADT)
구체적인 기능의 완성 과정을 언급하지 않고, 순수하게 기능이 무엇인지를 나열하는 것
추상화란 시스템의 간략화된 기술 또는 명세
ex) 자판기, 전자레인지 -> 기능만 나열한 것
자료구조 학습 순서
1. 자료구조의 ADT 정의
2. ADT를 근거로 자료구조를 활용하는 main 함수 정의
3. ADT를 근거로 자료구조 구현
복잡도 (Complexity)
- 알고리즘을 평가하는 두 가지 요소
- 시간 복잡도 (Time Complexity) -> 얼마나 빠른가?
- 공간 복잡도 (Space Complexity) -> 얼마나 메모리를 적게 쓰는가?
- 시간 복잡도 평가 방법
- 중심이 되는 특정 연산의 횟수를 세어 평가
- 데이터의 수에 대한 연산 횟수의 함수 T(n)을 구한다.
이진 탐색 알고리즘 (Binary Search Algorithm)
- 정렬 되어 있는 상태의 배열의 (시작 인덱스 값 + 끝 인덱스 값) / 2 = a 에 해당하는 인덱스를 먼저 탐색한다.
- 찾고자 하는 값이 a 인덱스에 있는 값보다 작은 경우 a 인덱스보다 (직전 인덱스 값 + 첫 인덱스 값) / 2에 해당하는 인덱스 탐색
- 탐색할 때까지 반복
-> 매 과정마다 탐색이 반씩 줄어듬 -> 순차 탐색보다 좋은 성능을 보인다.
이진 탐색 알고리즘 시간 복잡도
- 예시) 8이 1이 되기까지 2로 나눈 횟수 3회, 따라서 비교 연산 3회 진행
- 데이터가 1개 남았을 때, 마지막으로 비교 연산 1회 진행
- 일반화) n이 1이 되기까지 2로 나눈 횟수 k회, 따라서 비교 연산 k회 진행
- 데이터가 1개 남았을 때, 이때 마지막으로 비교 연산 1회 진행
- 총 -> k+1회 진행
Worst case의 시간 복잡도
- 최악의 경우에 대한 시간 복잡도 함수 T(n) = k + 1 -> T(k) = log2n + 1 (여기서 1은 생략할 수 있다.)
Big-O Notation
- T(n) = n^2 + 2n + 1에서 +1과 2n은 무시될 수 있다.
- 1 무시 이유 : n의 변화에 따른 T(n)의 변화 정도 판단이 목적
- 2n 무시 이유 : n이 증가할 수록 2n의 비율이 미미해진다.
- 따라서 T(n) = n^2 + 2n + 1에서 Big-O -> O(n^2)
T(n)에서 실제로 영향력을 끼치는 부분을 Big-O라고 함
- T(n) = n^2 + 2n + 9 -> O(n^2)
- T(n) = n^4 + n^3 + n^2 + 1 -> O(n^4)
- T(n) = 5n^3 + 3n^2 + 2n + 1 -> O(n^3)
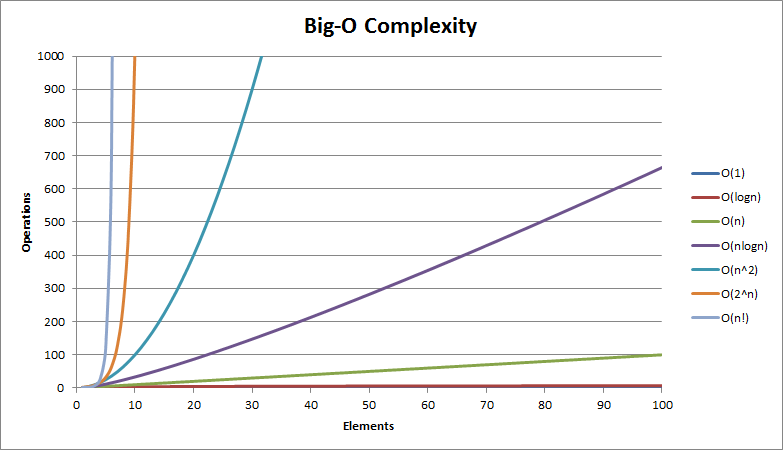
O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(n^3) < O(2^n)
'Algorithm > Study' 카테고리의 다른 글
| Linked List 구현 (0) | 2024.05.04 |
|---|---|
| 시간복잡도 (1) | 2024.02.11 |
자료구조 분류
1. 단순구조
- 정수
- 실수
- 문자
- 문자열
2. 선형구조 // 자료들 사이의 관계가 1:1 관계
- 리스트
- 스택
- 큐
3. 비선형구조 // 자료들 사이의 관계가 1다 or 다:다 관계
- 트리
- 그래프
4. 파일구조 // 서로 관련 있는 필드로 구성된 레코드의 집한인 파일에 대한 구조
- 순차파일
- 색인파일
- 직접파일
추상 자료형 (Abstract Data Type, ADT)
구체적인 기능의 완성 과정을 언급하지 않고, 순수하게 기능이 무엇인지를 나열하는 것
추상화란 시스템의 간략화된 기술 또는 명세
ex) 자판기, 전자레인지 -> 기능만 나열한 것
자료구조 학습 순서
1. 자료구조의 ADT 정의
2. ADT를 근거로 자료구조를 활용하는 main 함수 정의
3. ADT를 근거로 자료구조 구현
복잡도 (Complexity)
- 알고리즘을 평가하는 두 가지 요소
- 시간 복잡도 (Time Complexity) -> 얼마나 빠른가?
- 공간 복잡도 (Space Complexity) -> 얼마나 메모리를 적게 쓰는가?
- 시간 복잡도 평가 방법
- 중심이 되는 특정 연산의 횟수를 세어 평가
- 데이터의 수에 대한 연산 횟수의 함수 T(n)을 구한다.
이진 탐색 알고리즘 (Binary Search Algorithm)
- 정렬 되어 있는 상태의 배열의 (시작 인덱스 값 + 끝 인덱스 값) / 2 = a 에 해당하는 인덱스를 먼저 탐색한다.
- 찾고자 하는 값이 a 인덱스에 있는 값보다 작은 경우 a 인덱스보다 (직전 인덱스 값 + 첫 인덱스 값) / 2에 해당하는 인덱스 탐색
- 탐색할 때까지 반복
-> 매 과정마다 탐색이 반씩 줄어듬 -> 순차 탐색보다 좋은 성능을 보인다.
이진 탐색 알고리즘 시간 복잡도
- 예시) 8이 1이 되기까지 2로 나눈 횟수 3회, 따라서 비교 연산 3회 진행
- 데이터가 1개 남았을 때, 마지막으로 비교 연산 1회 진행
- 일반화) n이 1이 되기까지 2로 나눈 횟수 k회, 따라서 비교 연산 k회 진행
- 데이터가 1개 남았을 때, 이때 마지막으로 비교 연산 1회 진행
- 총 -> k+1회 진행
Worst case의 시간 복잡도
- 최악의 경우에 대한 시간 복잡도 함수 T(n) = k + 1 -> T(k) = log2n + 1 (여기서 1은 생략할 수 있다.)
Big-O Notation
- T(n) = n^2 + 2n + 1에서 +1과 2n은 무시될 수 있다.
- 1 무시 이유 : n의 변화에 따른 T(n)의 변화 정도 판단이 목적
- 2n 무시 이유 : n이 증가할 수록 2n의 비율이 미미해진다.
- 따라서 T(n) = n^2 + 2n + 1에서 Big-O -> O(n^2)
T(n)에서 실제로 영향력을 끼치는 부분을 Big-O라고 함
- T(n) = n^2 + 2n + 9 -> O(n^2)
- T(n) = n^4 + n^3 + n^2 + 1 -> O(n^4)
- T(n) = 5n^3 + 3n^2 + 2n + 1 -> O(n^3)

O(1) < O(log n) < O(n) < O(nlog n) < O(n^2) < O(n^3) < O(2^n)
'Algorithm > Study' 카테고리의 다른 글
| Linked List 구현 (0) | 2024.05.04 |
|---|---|
| 시간복잡도 (1) | 2024.02.11 |
